Home | Articles | Projects

Scheme to the Spec Part I: Concurrent Cycle Collection

by Matthew Plant

Scheme to the Spec (in Async Rust)

Scheme to the Spec is a series on the more complex, often overlooked aspects of programming language implementation.

In this series we will dive deep into my work-in-progress implementation of R6RS scheme, scheme-rs, an implementation designed to integrate seamlessly with the async-rust ecosystem.

Our first article discusses how to implement Garbage-Collected smart pointers that we can use both within the interpreter and the interfacing Rust code. In later articles we will discuss topics such as tail call optimizations, implementing continuations, and syntax transformers. Our final article will be implementing on-stack replacement with LLVM.

Part I: Garbage Collected Smart Pointers via Concurrent Cycle Collection

Ten years ago I wrote an article on how to implement a conservative garbage collector for C, and I got a lot of constructive criticism regarding the actual usefulness of the code presented. It only makes sense that on the ten-year anniversary of publishing I should try to fix my error by writing a garbage collector that is precise, does not make assumptions, and (hopefully) actually works.

Table of contents

  1. The Gc<T> smart pointer
    1. Scaffolding and allocation
      1. Variance
      2. Drop checking
  2. Thread-safe interior mutability
    1. Semaphores
    2. Read/write guards
  3. Garbage collection
    1. Cycles
    2. Synchronous cycle collection
    3. The Trace trait and derive macro
    4. Deallocation
    5. Extending from synchronous to concurrent
      1. The mutation buffer
      2. The Cyclical Reference Count
      3. The safety phase
        1. Σ-test
        2. Δ-test
      4. Cleaning up
      5. Misc helper functions
    6. Bringing it all together
  4. Testing
  5. Footnotes

1. The Gc<T> smart pointer

Before we can start writing code, we have to figure out what goals we want to accomplish. More specifically, what do we want our Gc<T> type to do? How does it behave? What kind of data can it contain?

I want the Gc<T> type to work as follows:

Why a RwLock and not a Mutex? RwLocks are not always ideal as a lock, so we need a particularly good justification for choosing them. Since read and write locks are given access in a FIFO queue and neither has a higher priority than the other, acquiring a write lock can take a disproportionate amount of time. But, let’s consider the language we are implementing: a functional language with relatively few concurrent writes.

In Scheme, writes occur most often when adding a variable to a lexical environment, and by and large that happens synchronously. For example, in the following snippet

(define pi 3.1415)
(define e  2.7182)

write locks are acquired on the environment sequentially, and thus the process does not need to wait.

RwLocks would be a poor choice for Scheme code with multiple threads all reading and writing to a global variable. This pattern is just not very common in functional programming where message passing is vastly preferred.

Now that we have an idea as to how our smart pointer should behave, we can begin our implementation.

1.1. Scaffolding and allocation

Our Gc type will be composed of three separate types:

To begin, we have no extra information we need to store in GcHeader, so we can knock it out quickly:

struct GcHeader;

GcInner<T> is just the header and the data, so it is equally simple:

struct GcInner<T> {
    header: GcHeader,
    data: T,
}

We are ready to put together our Gc<T> type. One might define it rather simply as the following:

struct Gc<T> {
    ptr: *mut T,
}

Unfortunately, this definition has two major problems:

1.1.1. Variance

This struct does not pass through subtyping relationships on T; i.e., this structure is invariant over T. Ideally, for every two type parameters A and B, if A is a subtype of B we would also like Gc<A> to be a subtype of Gc<B> because we want a Gc<T> to behave as close to a T as possible. The reason this occurs is because pointer types in Rust are invariant, and thus our wrapper type will be as well.

We can fix this by using a NonNull<T> pointer type, which is covariant over T. Additionally, this ensures that any Gc we successfully create will never contain a null pointer, which is a plus.

In reality, variance is not particularly useful for our struct since we only support types that are 'static, and most subtyping relationships in Rust regard references. However, there are a few times when it may come up 1, so there is no reason to not support it.

1.1.2. Drop checking

As it’s specified now, the Rust compiler is forced to assume that any Gc<T> will be strictly out-lived by the underlying data. For our data type this not the case. Although a lot of Gcs represent references to data, some Gcs represent the entire lifetime - they represent the data itself. Therefore, dropping a Gc can potentially drop the underlying T value. The Rust compiler needs to know about this in order to perform its drop check analysis, or else potentially unsound code can be constructed 2.

In order to indicate this information, we can use a PhantomData, a neat wrapper type that indicates to the compiler that our data type should behave as if it has ownership over a type T.

With these two data types we can put together our Gc:

/// A Garbage-Collected smart pointer with interior mutability.
pub struct Gc<T> {
    ptr: NonNull<GcInner<T>>,
    marker: PhantomData<GcInner<T>>,
}

impl<T> Gc<T> {
    pub fn new(data: T) -> Gc<T> {
        Self {
            ptr: NonNull::from(Box::leak(Box::new(GcInner {
                header: GcHeader::default(),
                data,
            }))),
            marker: PhantomData,
        }
    }
}

The new function is rather straightforward but worth commenting on. The easiest way to allocate a pointer in Rust is to use the Box::new function to allocate space and copy data onto the heap, and then use the Box::leak function to consume the box without running its destructor and returning us a dangling pointer.

2. Thread-safe interior mutability

After our data is allocated, we need a way to read and write to it in a thread-safe manner. By default, Rust assumes that for the lifetime an immutable reference is held, the data referenced to will not be modified. We would like to opt out of that assumption. To that end, we must use the UnsafeCell wrapper.

Of course, we want to ensure that if someone is trying to read the data behind a a Gc that no one is trying to modify it at the same time, as that would be unsound.

Additionally, we are going to tell Rust that it should trust us to implement these rules in a thread-safe manner. Our GcInner type now looks like the following:

pub struct GcInner<T: ?Sized> {
    header: UnsafeCell<GcHeader>,
    data: UnsafeCell<T>,
}

unsafe impl<T: ?Sized + Send> Send for GcInner<T> {}
unsafe impl<T: ?Sized + Sync> Sync for GcInner<T> {}

// (also necessary)
unsafe impl Send for GcHeader {}
unsafe impl Sync for GcHeader {}

This sets up our Gc<T> type to have thread-safe interior mutability. We must now implement it.

2.1. Semaphores

A Semaphore is a way to control access to a resource. Essentially, it is an array of N slots that each process is allowed to claim ownership of. If all N slots are claimed, then processes must queue up and wait for the processes with ownership to relinquish them.

Acquire(Semaphore<N>) -> Option<Permit>
Release(Permit)

(both of these operations are atomic)

The ordering of these slots is irrelevant. Processes are only concerned with having ownership of a slot or not. If the Semaphore has only one slot, you can make this value behave exactly like a typical Mutex:

Lock(Semaphore) -> Permit:
    loop:
        match Acquire(Semaphore):
            Some(Permit) => return Permit,

If we were to change our semaphore to have N > 1 slots, we need to add another atomic operation in order to properly mimic our Mutex:

AcquireMany(Semaphore, NumSlots) -> Option<Permit>

Locking is pretty much the same but instead of attempting to acquire one slot we attempt to acquire all N.

We don’t have to always lock a variable. We can use semaphores with N > 1 to mimic Rust’s safety rules - we can have an unlimited number of immutable references OR one single mutable reference, and never both. The trick is to have our reads only acquire one slot and to have our writes acquire all N.

To implement this, we’re going to use tokio’s Semaphore, which interfaces well with async rust. Let’s add it to GcHeader:

struct GcHeader {
    semaphore: tokio::sync::Semaphore,
}

2.2. Read/write guards

We need some types to represent our acquired resources. In Rust, this done with Guards. Guards are structs that:

pub struct GcReadGuard<'a, T: ?Sized> {
    _permit: tokio::sync::SemaphorePermit<'a>,
    data: *const T,
    marker: PhantomData<&'a T>,
}

impl<T: ?Sized> Deref for GcReadGuard<'_, T> {
    type Target = T;

    fn deref(&self) -> &T {
        unsafe { &*self.data }
    }
}

unsafe impl<T: ?Sized + Send> Send for GcReadGuard<'_, T> {}
unsafe impl<T: ?Sized + Sync> Sync for GcReadGuard<'_, T> {}

pub struct GcWriteGuard<'a, T: ?Sized> {
    _permit: tokio::sync::SemaphorePermit<'a>,
    data: *mut T,
    marker: PhantomData<&'a mut T>,
}

impl<T> Deref for GcWriteGuard<'_, T: ?Sized> {
    type Target = T;

    fn deref(&self) -> &T {
        unsafe { &*self.data }
    }
}

impl<T> DerefMut for GcWriteGuard<'_, T: ?Sized> {
    fn deref_mut(&mut self) -> &mut T {
        unsafe { &mut *self.data }
    }
}

unsafe impl<T: ?Sized + Send> Send for GcWriteGuard<'_, T> {}
unsafe impl<T: ?Sized + Sync> Sync for GcWriteGuard<'_, T> {}

Again, you will notice that in both of these structs we use the same trick to ensure the desired variance (covariance) over each of the guards type parameters.

Since we use the tokio semaphore, we can create futures that await the acquisition of a permit:

impl<T> Gc<T> {
    /// Acquire a read lock for the object
    pub async fn read(&self) -> GcReadGuard<'_, T> {
        unsafe {
            let _permit = (*self.ptr.as_ref().header.get())
                .semaphore
                .acquire()
                .await
                .unwrap();
            let data = &*self.ptr.as_ref().data.get() as *const T;
            GcReadGuard {
                _permit,
                data,
                marker: PhantomData,
            }
        }
    }

    /// Acquire a write lock for the object
    pub async fn write(&self) -> GcWriteGuard<'_, T> {
        unsafe {
            let _permit = (*self.ptr.as_ref().header.get())
                .semaphore
                .acquire_many(MAX_READS)
                .await
                .unwrap();
            let data = &mut *self.ptr.as_ref().data.get() as *mut T;
            GcWriteGuard {
                _permit,
                data,
                marker: PhantomData,
            }
        }
    }
}

This gives us a heap allocated object with thread-safe interior mutability that lives forever. Our last task is to make it mortal.

3. Garbage collection

There are two main techniques for determining if allocated objects should be freed; tracing and reference counting. Besides practical differences in performance and memory overhead, they differ in what information they take as input:

Determining an object’s reference count in Rust is fairly straightforward. In Rust, an object’s reference count is equal to the difference of clones and drops plus one3. This is because Rust has an affine type system for objects that do not implement Copy, which means that an object that does not implement Copy can be moved at most once. Therefore, moves do not affect the reference count of an object. 4

To contrast this, figuring out the root objects in Rust is difficult. It’s certainly possible5, but reference counts are much easier to work with. This is why Rust’s default automatic memory management types, Rc and Arc, are both reference counted and can be easily implemented in user code. Therefore, we will use reference counting.

But reference counting has a key problem. If it didn’t we wouldn’t have a reason to implement our own type.

3.1. Cycles

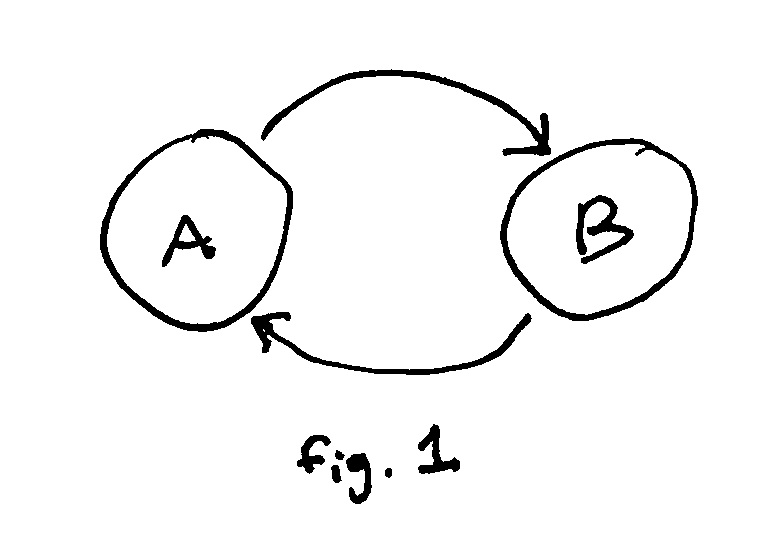
A simple cyclic data structure consisting of two nodes: A and B, and two edges: AB and BA

An object can be unreachable but still have a positive reference count. This is because our Gc type allows for the creation of cyclical data structures (see fig. 1). Such data structures are pretty common to, especially in functional languages like Scheme. In order to ensure that cyclical data structures are collected appropriately, we will be implementing Concurrent Cycle Collection in Reference Counted Systems by David F. Bacon and V.T. Rajan 6, an algorithm for automatically detecting and collecting cycles in reference counted data structures.

3.2. Synchronous cycle collection

Before we implement concurrent cycle detection, let’s start with synchronous. Here is the code listing for the synchronous cycle collection algorithm:

Increment(s)
    RC(S) = RC(S) + 1
    color(S) = black

ScanRoots()
    for S in Roots
        Scan(s)

Decrement(S) 
    RC(S) = RC(S) - 1
    if (RC(S) == 0) 
        Release(S) 
    else 
        PossibleRoot(S)

CollectRoots()
    for S in Roots
        remove S from Roots
        buffered(S) = false
        CollectWhite(S)

Release(S)
    for T in children(S)
        Decrement(T)
    color(S) = black
    if (! buffered(S))
        Free(S)

MarkGray(S)
    if (color(S) != gray)
        color(S) = gray
        for T in children(S)
            Rc(T) = RC(T) - 1
            MarkGray(T)

PossibleRoot(S)
    if (color(S) != purple)
        color(S) = purple
        if (! buffered(S))
            buffered(S) = true
            append S to Roots

Scan(S)
    if (color(S) == gray)
        if (RC(S) > 0)
            ScanBlack(S)
        else
            color(S) = white
            for T in children(S)
                Scan(T)

CollectCycles()
    MarkRoots()
    ScanRoots()
    CollectRoots()

ScanBlack(S)
    color(S) = black
    for T in children(S)
        RC(T) = RC(T) + 1
        if (color(T) != black)
            ScanBlack(T)

MarkRoots()
    for S in Roots
        if (color(S) == purple)
            MarkGray(S)
        else
            buffered(S) = false
            remove S from Roots
            if (color(S) == black and RC(S) == 0)
                Free(S)

CollectWhite(S)
    if (color(S) == white and !buffered(S))
        color(S) = black
        for T in children(S)
            CollectWhite(T)
        Free(S)

Everyone loves to trust code at face value, but how does this actually work? I encourage you to read the paper, but I will summarize the operation leaving out some very important details.

Cycle Collection relies on this key insight: if you were to perform a drop on every node in a cycle, that cycle will be garbage if the remaining ref count of every node in that cycle is zero. This kind of makes sense intuitively, what we’re basically saying here is that if we somehow already knew that a data structure was cyclic, we could just manually sever an outgoing reference for some random node and the cascade of decrementing reference counts would cleanly free the whole data structure.

With this in mind, we can can construct an efficient algorithm to collect cyclical garbage. We’ll color the nodes in different colors as they pass through different stages

There is one thing in particular that is not immediately clear as to how we are going to implement. How do we iterate over the children? We haven’t put any bounds on the T in our Gc<T> beyond that it has to be 'static. Well, until Rust gains a more powerful reflection story, we are going to have to add a classic Trait plus derive macro combo.

3.3. The Trace trait and derive macro

Let’s define the trait we need to implement the above code. We need a function that matches the following form:

for T in children(S):
    F(T)

We can extract two type parameters from this statement: S, and F(T) where T == S. Therefore, the function we want will have the form fn for_each_children(S, impl FnMut(S)).

It’s not entirely obvious at first glance, but there is another function that we must pay attention to: free. The free function presented in the above code listing does not correspond to how memory is freed in Rust. That is because this code assumes that when we free code we are not running any of its members destructors. But we do want to run our destructors. At least, we want to run the destructor if the type is not a Gc. We’re going to have to add a finalize function to handle a custom drop routine:

unsafe trait Trace: 'static {
    unsafe fn visit_children(&self, visitor: unsafe fn(OpaqueGcPtr));
    
    unsafe fn finalize(&mut self) {
        drop_in_place(self as *mut Self);
    }
}

These two things are in fact the only two things our collection algorithm cares about in regards to Gc’s data. Therefore, whenever we’re in the context of the collection algorithm, we will cast our Gc’s into a trait object:

type OpaqueGc = GcInner<dyn Trace>;
pub type OpaqueGcPtr = NonNull<OpaqueGc>;

impl<T: Trace> Gc<T> {
    pub unsafe fn as_opaque(&self) -> OpaqueGcPtr {
        self.ptr as OpaqueGcPtr
    }
}

With the Trace trait defined, we can implement it for some primitive types to give us some building blocks with which to implement composite structures. A good starting point will be Rust’s std library, since those data structures are used throughout the entire Rust ecosystem. I won’t provide all of the ones I implemented, but here are a few:

unsafe trait GcOrTrace: 'static {
    unsafe fn visit_or_recurse(&self, visitor: unsafe fn(OpaqueGcPtr));

    unsafe fn finalize_or_skip(&mut self);
}

unsafe impl<T: Trace> GcOrTrace for Gc<T> {
    unsafe fn visit_or_recurse(&self, visitor: unsafe fn(OpaqueGcPtr)) {
        visitor(self.as_opaque())
    }

    unsafe fn finalize_or_skip(&mut self) {}
}

unsafe impl<T: Trace + ?Sized> GcOrTrace for T {
    unsafe fn visit_or_recurse(&self, visitor: unsafe fn(OpaqueGcPtr)) {
        self.visit_children(visitor);
    }

    unsafe fn finalize_or_skip(&mut self) {
        self.finalize();
    }
}

unsafe impl<T> Trace for Vec<T>
where
    T: GcOrTrace,
{
    unsafe fn visit_children(&self, visitor: unsafe fn(OpaqueGcPtr)) {
        for child in self {
            child.visit_or_recurse(visitor);
        }
    }

    unsafe fn finalize(&mut self) {
        for mut child in std::mem::take(self).into_iter().map(ManuallyDrop::new) {
            child.finalize_or_skip();
        }
    }
}

unsafe impl<T> Trace for Option<T>
where
    T: GcOrTrace,
{
    unsafe fn visit_children(&self, visitor: unsafe fn(OpaqueGcPtr)) {
        if let Some(inner) = self {
            inner.visit_or_recurse(visitor);
        }
    }

    unsafe fn finalize(&mut self) {
        if let Some(inner) = self {
            inner.finalize_or_skip();
        }
    }
}

unsafe impl<T> Trace for std::sync::Arc<T>
where
    T: GcOrTrace,
{
    unsafe fn visit_children(&self, visitor: unsafe fn(OpaqueGcPtr)) {
         self.as_ref().visit_or_recurse(visitor);
    }
}

If you are able to immediately spot the error in the code above, you are much smarter than I am. I hope you at least have the courtesy to be less good looking. Anyway, this code isn’t correct with our current set of assumptions. And that’s due to the implementation for Arc, which recurses into its data.

The problem is that we are basically disregarding the reference count of the Arc. Consider the following structure:

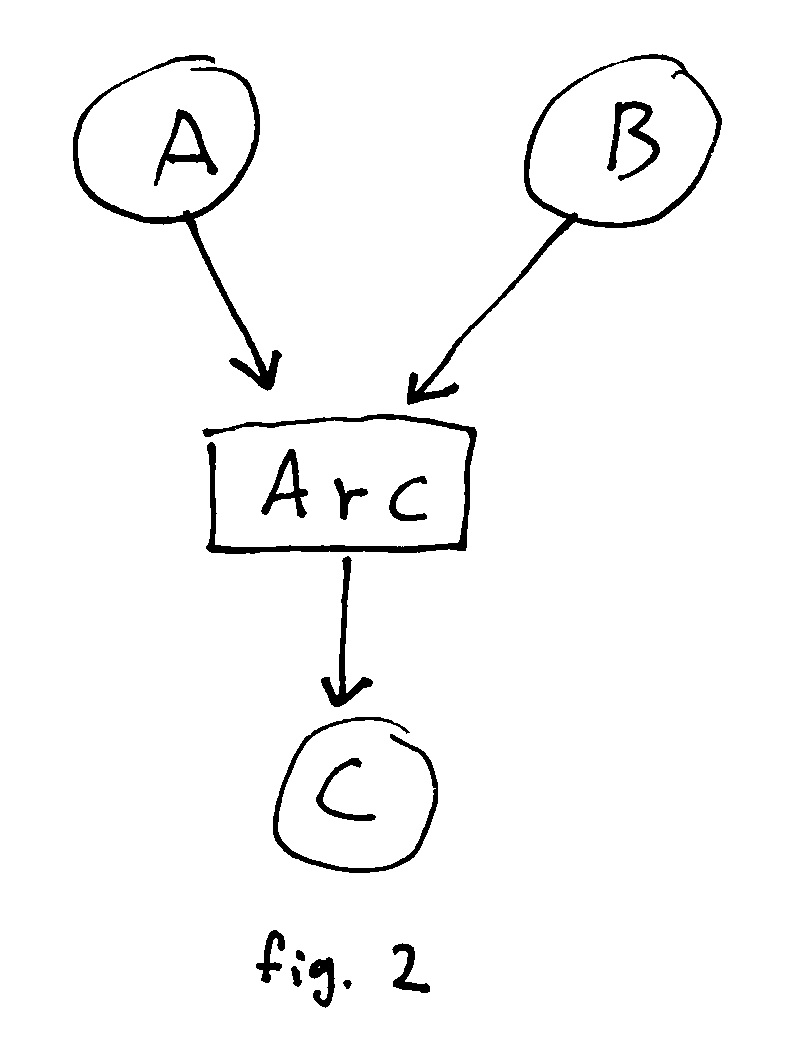
A data structure with three nodes: A, B, C and Arc, with three edges: A->Arc, B->Arc, Arc->C

In this case, dropping A results in the immediate dropping of C while a dangling reference from B remains. Essentially, the Arc collapses all of the incoming references to C into one.

Here is the correct code for Arc. Part of what makes this code correct is that we added an explanation, so be sure to always do that.

unsafe impl<T> Trace for std::sync::Arc<T>
where
    T: ?Sized + 'static,
{
    unsafe fn visit_children(&self, _visitor: unsafe fn(OpaqueGcPtr)) {
        // We cannot visit the children for an Arc, as it may lead to situations
        // were we incorrectly decrement a child twice.
        // An Arc wrapping a Gc effectively creates an additional ref count for
        // that Gc that we cannot access.
    }
}

Another important thing to discuss is the operation of finalize for Vec (and other container types):

unsafe impl<T> Trace for Vec<T>
where
    T: GcOrTrace,
{
    unsafe fn finalize(&mut self) {
        for mut child in std::mem::take(self).into_iter().map(ManuallyDrop::new) {
            child.finalize_or_skip();
        }
    }
}

Our finalization here is pretty particular: we take the memory allocated by the Vec, convert it into and owned iterator so we can be sure there are no dangling references to child that drop may be run on, and drop the children manually. The child is moved into a ManuallyDrop so that if a panic occurrs within the finalization its destructor will not be run on unwind.

I am not going to get too into the Trait derive proc macro code as it’s not particularly interesting and quite long. But it’s important to note what it is actually doing for any given type T:

If you would like to see how this is done, the code is available here.

3.4. Deallocation

The free function needs to call std::alloc::dealloc to free the allocated memory. This function takes a Layout (a size and alignment). How do we find this for our opaque dyn Trace pointer? Turns out the size and alignment of the underlying data is part of Rust’s vtable. So, we can just call Layout::for_value on our reference and create one. Here’s the resulting free function:

unsafe fn trace<'a>(s: OpaqueGcPtr) -> &'a mut dyn Trace {
    &mut *s.as_ref().data.get()
}

unsafe fn free(s: OpaqueGcPtr) {
    // Safety: No need to acquire a permit, s is guaranteed to be garbage.
    let trace = trace(s);
    let layout = Layout::for_value(trace);
    trace.finalize();
    std::alloc::dealloc(s.as_ptr() as *mut u8, layout);
}

3.5. Extending from synchronous to concurrent

If we wish to move our collection into a separate thread, we are somehow going to have to deal with two things:

In order to explain how each of these things are dealt with, let’s take a look at our final GcHeader:

pub struct GcHeader {
    rc: usize,
    crc: usize,
    color: Color,
    buffered: bool,
    semaphore: Semaphore,
}

enum Color {
    /// In use or free
    Black,
    /// Possible member of a cycle
    Gray,
    /// Member of a garbage cycle
    White,
    /// Possible root of cycle
    Purple,
    /// Candidate cycle undergoing Σ-computation
    Red,
    /// Candidate cycle awaiting epoch boundary
    Orange,
}

This header is quite large and therefore a lot of overhead. It can be made smaller with some tricks, such as assuming that most nodes will not have more than 255 reference counts and storing overflowing ref counts externally, but we will ignore those tricks for now.

3.5.1. The mutation buffer

You will notice that the ref counts for our Gc type are not atomic. This is because our concurrent algorithm requires a constraint: only one thread at a time can ever modify the ref count, or indeed any field in the GcHeader except for semaphore (which is already thread safe). This gives our garbage collection process exclusive read and write access to most of the header.

What gives? How does that work? Isn’t this algorithm supposed to be concurrent? We don’t want decrementing or incrementing ref counts to wait on the completion of the GC process. That would make our drop and clone functions blocking, which would gum up our whole system.

The solution is the mutation buffer, an unbounded channel that lets us buffer incremements and decrements to be handled by our collection process as it pleases.

This wil allow our collector to stop processing incremements and decrements at any time and effectively have a snapshot of the system without causing any pauses in other threads. Since the buffer is unbounded, calling send is a non-blocking, sync operation:

#[derive(Copy, Clone)]
struct Mutation {
    kind: MutationKind,
    gc: NonNull<OpaqueGc>,
}

impl Mutation {
    fn new(kind: MutationKind, gc: NonNull<OpaqueGc>) -> Self {
        Self { kind, gc }
    }
}

unsafe impl Send for Mutation {}
unsafe impl Sync for Mutation {}

#[derive(Copy, Clone)]
enum MutationKind {
    Inc,
    Dec,
}

/// Instead of mutations being atomic (via an atomic variable), they're buffered into
/// "epochs", and handled by precisely one thread.
struct MutationBuffer {
    mutation_buffer_tx: UnboundedSender<Mutation>,
    mutation_buffer_rx: Mutex<Option<UnboundedReceiver<Mutation>>>,
}

unsafe impl Sync for MutationBuffer {}

impl Default for MutationBuffer {
    fn default() -> Self {
        let (mutation_buffer_tx, mutation_buffer_rx) = unbounded_channel();
        Self {
            mutation_buffer_tx,
            mutation_buffer_rx: Mutex::new(Some(mutation_buffer_rx)),
        }
    }
}

static MUTATION_BUFFER: OnceLock<MutationBuffer> = OnceLock::new();

fn inc_rc<T: Trace>(gc: NonNull<GcInner<T>>) {
    // Disregard any send errors. If the receiver was dropped then the process
    // is exiting and we don't care if we leak.
    let _ = MUTATION_BUFFER
        .get_or_init(MutationBuffer::default)
        .mutation_buffer_tx
        .send(Mutation::new(MutationKind::Inc, gc as NonNull<OpaqueGc>));
}

fn dec_rc<T: Trace>(gc: NonNull<GcInner<T>>) {
    // Disregard any send errors. If the receiver was dropped then the process
    // is exiting and we don't care if we leak.
    let _ = MUTATION_BUFFER
        .get_or_init(MutationBuffer::default)
        .mutation_buffer_tx
        .send(Mutation::new(MutationKind::Dec, gc as NonNull<OpaqueGc>));
}

And now we finally can implement Clone and Drop for Gc<T>:

impl<T: Trace> Clone for Gc<T> {
    fn clone(&self) -> Gc<T> {
        inc_rc(self.ptr);
        Self {
            ptr: self.ptr,
            marker: PhantomData,
        }
    }
}

impl<T: Trace> Drop for Gc<T> {
    fn drop(&mut self) {
        dec_rc(self.ptr);
    }
}

This also presents a structure for our collection process: wait for some increments and decrements, process them, then decide if we want to try to perform a collection:

static COLLECTOR_TASK: OnceLock<JoinHandle<()>> = OnceLock::new();

pub fn init_gc() {
    // SAFETY: We DO NOT mutate MUTATION_BUFFER, we mutate the _interior once lock_.
    let _ = MUTATION_BUFFER.get_or_init(MutationBuffer::default);
    let _ = COLLECTOR_TASK
        .get_or_init(|| tokio::task::spawn(async { unsafe { run_garbage_collector().await } }));
}

const MUTATIONS_BUFFER_DEFAULT_CAP: usize = 10_000;

async unsafe fn run_garbage_collector() {
    let mut last_epoch = Instant::now();
    let mut mutation_buffer_rx = MUTATION_BUFFER
        .get_or_init(MutationBuffer::default)
        .mutation_buffer_rx
        .lock()
        .unwrap()
        .take()
        .unwrap();
    let mut mutation_buffer: Vec<_> = Vec::with_capacity(MUTATIONS_BUFFER_DEFAULT_CAP);
    loop {
        epoch(
            &mut last_epoch, 
            &mut mutation_buffer_rx,
            &mut mutation_buffer
        ).await;
        mutation_buffer.clear();
    }
}

async unsafe fn epoch(
    last_epoch: &mut Instant, 
    mutation_buffer_rx: &mut Vec<Mutation>,
    mutation_buffer: &mut Vec<Mutation>
) {
    process_mutation_buffer(mutation_buffer_rx, mutation_buffer).await;
    let duration_since_last_epoch = Instant::now() - *last_epoch;
    if duration_since_last_epoch > Duration::from_millis(100) {
        // This could be cancelled at shutdown, proper code should exit
        // if awaiting the task yields an error.
        tokio::task::spawn_blocking(|| unsafe { process_cycles() })
            .await
            .unwrap();
        *last_epoch = Instant::now();
    }
}

/// SAFETY: this function is _not reentrant_, may only be called by once per epoch,
/// and must _complete_ before the next epoch.
async unsafe fn process_mutation_buffer(
    mutation_buffer_rx: &mut UnboundedReceiver<Mutation>,
    mutation_buffer: &mut Vec<Mutation>
) {
    // It is very important that we do not delay any mutations that 
    // have occurred at this point by an extra epoch. 
    let to_recv = mutation_buffer_rx.len();
    mutation_buffer_rx
        .recv_many(mutation_buffer, to_recv)
        .await;

    for mutation in mutation_buffer {
        match mutation.kind {
            MutationKind::Inc => increment(mutation.gc),
            MutationKind::Dec => decrement(mutation.gc),
        }
    }
}

3.5.2. The Cyclical Reference Count

You will notice in the GcHeader we added a second reference counting field called the CRC. This is distinguished from the “true” reference count, the RC, by being the hypothetical reference count of the node that has perhaps become invalidated during the epoch. We can modify the code listing to create the following functions that use the CRC instead 7:

// SAFETY: These values can only be accessed by one thread at once.
static mut ROOTS: Vec<OpaqueGcPtr> = Vec::new();
static mut CYCLE_BUFFER: Vec<Vec<OpaqueGcPtr>> = Vec::new();
static mut CURRENT_CYCLE: Vec<OpaqueGcPtr> = Vec::new();

unsafe fn increment(s: OpaqueGcPtr) {
    *rc(s) += 1;
    scan_black(s);
}

unsafe fn decrement(s: OpaqueGcPtr) {
    *rc(s) -= 1;
    if *rc(s) == 0 {
        release(s);
    } else {
        possible_root(s);
    }
}

unsafe fn release(s: OpaqueGcPtr) {
    for_each_child(s, decrement);
    *color(s) = Color::Black;
    if !*buffered(s) {
        free(s);
    }
}

unsafe fn possible_root(s: OpaqueGcPtr) {
    scan_black(s);
    *color(s) = Color::Purple;
    if !*buffered(s) {
        *buffered(s) = true;
        (&raw mut ROOTS).as_mut().unwrap().push(s);
    }
}

// SAFETY: No function called by mark_roots may access ROOTS
unsafe fn mark_roots() {
    let mut new_roots = Vec::new();
    for s in (&raw const ROOTS).as_ref().unwrap().iter() {
        if *color(*s) == Color::Purple && *rc(*s) > 0 {
            mark_gray(*s);
            new_roots.push(*s);
        } else {
            *buffered(*s) = false;
            if *rc(*s) == 0 {
                free(*s);
            }
        }
    }
    ROOTS = new_roots;
}

unsafe fn scan_roots() {
    for s in (&raw const ROOTS).as_ref().unwrap().iter() {
        scan(*s)
    }
}

unsafe fn collect_roots() {
    for s in std::mem::take((&raw mut ROOTS).as_mut().unwrap()) {
        if *color(s) == Color::White {
            collect_white(s);
            let current_cycle = std::mem::take((&raw mut CURRENT_CYCLE).as_mut().unwrap());
            (&raw mut CYCLE_BUFFER)
                .as_mut()
                .unwrap()
                .push(current_cycle);
        } else {
            *buffered(s) = false;
        }
    }
}

unsafe fn mark_gray(s: OpaqueGcPtr) {
    if *color(s) != Color::Gray {
        *color(s) = Color::Gray;
        *crc(s) = *rc(s) as isize;
        for_each_child(s, |t| {
            mark_gray(t);
            if *crc(t) > 0 {
                *crc(t) -= 1;
            }
        });
    }
}

unsafe fn scan(s: OpaqueGcPtr) {
    if *color(s) == Color::Gray {
        if *crc(s) == 0 {
            *color(s) = Color::White;
            for_each_child(s, scan);
        } else {
            scan_black(s);
        }
    }
}

unsafe fn scan_black(s: OpaqueGcPtr) {
    if *color(s) != Color::Black {
        *color(s) = Color::Black;
        for_each_child(s, scan_black);
    }
}

unsafe fn collect_white(s: OpaqueGcPtr) {
    if *color(s) == Color::White {
        *color(s) = Color::Orange;
        *buffered(s) = true;
        (&raw mut CURRENT_CYCLE).as_mut().unwrap().push(s);
        for_each_child(s, collect_white);
    }
}

3.5.3. The safety phase

Because of concurrent mutations to the edges of our graph, there is a possibility that our mark algorithm will produce results that are incorrect. Therefore, we divide our collection algorithm into two phases:

The correctness of this approach relies on another key insight: any mutation that occurs while we are marking our cycles must appear in the next epoch. Therefore, we need to check that no external node adds an edge to our potential cycle over the current and next epoch.

We have two tests for this, corresponding to the current and next epoch respectively:

3.5.3.1. Σ-test

The sigma test requires preparation. In essence preparation boils down to using the same algorithm as MarkGray, but we are restricting it to only the nodes of a given cycle:

unsafe fn sigma_preparation() {
    for c in (&raw const CYCLE_BUFFER).as_ref().unwrap() {
        for n in c {
            *color(*n) = Color::Red;
            *crc(*n) = *rc(*n);
        }
        for n in c {
            for_each_child(*n, |m| {
                if *color(m) == Color::Red && *crc(m) > 0 {
                    *crc(m) -= 1;
                }
            });
        }
        for n in c {
            *color(*n) = Color::Orange;
        }
    }
}

At the end of prepartion, if any of the circular reference counts are greater than zero, the graph is live. We check this in the next epoch:

unsafe fn sigma_test(c: &[OpaqueGcPtr]) -> bool {
    for n in c {
        if *crc(*n) > 0 {
            return false;
        }
    }
    true
}

The reason that this test is called the “sigma” test is because the sum of the circular reference counts will remain zero in a garbage cycle.

3.5.3.2. Δ-test

If any node’s reference count is incremented in the next epoch, it will be colored black and fail the delta test:

unsafe fn delta_test(c: &[OpaqueGcPtr]) -> bool {
    for n in c {
        if *color(*n) != Color::Orange {
            return false;
        }
    }
    true
}

3.5.4. Cleaning up

If a candidate cycle fails either of the tests, we want to make sure to properly re-color the nodes. There’s an additional heuristic that adds some nodes back to the roots list.

unsafe fn refurbish(c: &[OpaqueGcPtr]) {
    for (i, n) in c.iter().enumerate() {
        match (i, *color(*n)) {
            (0, Color::Orange) | (_, Color::Purple) => {
                *color(*n) = Color::Purple;
                unsafe {
                    (&raw mut ROOTS).as_mut().unwrap().push(*n);
                }
            }
            _ => {
                *color(*n) = Color::Black;
                *buffered(*n) = false;
            }
        }
    }
}

If a candidate cycle passes both tests, we need to free it and decrement any outgoing reference counts. This is pretty straightforward:

unsafe fn cyclic_decrement(m: OpaqueGcPtr) {
    if *color(m) != Color::Red {
        if *color(m) == Color::Orange {
            *rc(m) -= 1;
            *crc(m) -= 1;
        } else {
            decrement(m);
        }
    }
}


unsafe fn free_cycle(c: &[OpaqueGcPtr]) {
    for n in c {
        *color(*n) = Color::Red;
    }
    for n in c {
        for_each_child(*n, cyclic_decrement);
    }
    for n in c {
        free(*n);
    }
}

3.5.5. Misc helper functions

Before we put everything together, let’s briefly talk about some of the helper functions:

unsafe fn color<'a>(s: OpaqueGcPtr) -> &'a mut Color {
    &mut (*s.as_ref().header.get()).color
}

unsafe fn rc<'a>(s: OpaqueGcPtr) -> &'a mut usize {
    &mut (*s.as_ref().header.get()).rc
}

unsafe fn buffered<'a>(s: OpaqueGcPtr) -> &'a mut bool {
    &mut (*s.as_ref().header.get()).buffered
}

unsafe fn semaphore<'a>(s: OpaqueGcPtr) -> &'a Semaphore {
    &(*s.as_ref().header.get()).semaphore
}

fn acquire_permit(semaphore: &'_ Semaphore) -> SemaphorePermit<'_> {
    loop {
        if let Ok(permit) = semaphore.try_acquire() {
            return permit;
        }
    }
}

unsafe fn for_each_child(s: OpaqueGcPtr, visitor: unsafe fn(OpaqueGcPtr)) {
    let permit = acquire_permit(semaphore(s));
    (*s.as_ref().data.get()).visit_children(visitor);
    drop(permit);
}

These are all pretty straightforward, but you may notice that we acquire a read lock on the data for the Gc when we call for_each_child. I couldn’t find any mention of it in the paper but it has the assumption that pointer store and loads are atomic.

The way this is implemented is not ideal as the permit is acquired for the lifetime of the visit_children function. A better approach would be to collect all of the OpaqueGcPtrs into a buffer and traverse them after releasing the permit.

3.6. Bringing it all together

Finally, we can write the last of our functions:

unsafe fn process_cycles() {
    free_cycles();
    collect_cycles();
    sigma_preparation();
}

unsafe fn collect_cycles() {
    mark_roots();
    scan_roots();
    collect_roots();
}

4. Testing

Garbage Collection is very hard to properly test. Often times testing is done via metrics: For example, there were x1 allocations time t1, there were x2 allocations at time t2, t1 < t2 and x1 > x2 so the garbage collector did some work over t2 - t1.

Because we are building our garbage collector on top of a system that already supports reference counted smart pointers, we can use an Arc to analyse the operation of our collection algorithms. By analyzing the strong reference count of an Arc embedded in a garbage cyclical data structure, we can determine that our cycle was properly destroyed if the strong reference count for the Arc decreases.

We could also do this with our own Gc type, but as we have established only one thread can ever read the reference count. Therefore, if we want to adapt our unit tests to include the collector running in parallel, we cannot use them.

This is a pretty nice consequence of allowing Arc in our Gc<T>s, we can add a very simple unit test to our code. It is insufficient amount of testing, but this article is already quite long, so I will leave the rest up to you dear reader.

Consider the following structure:

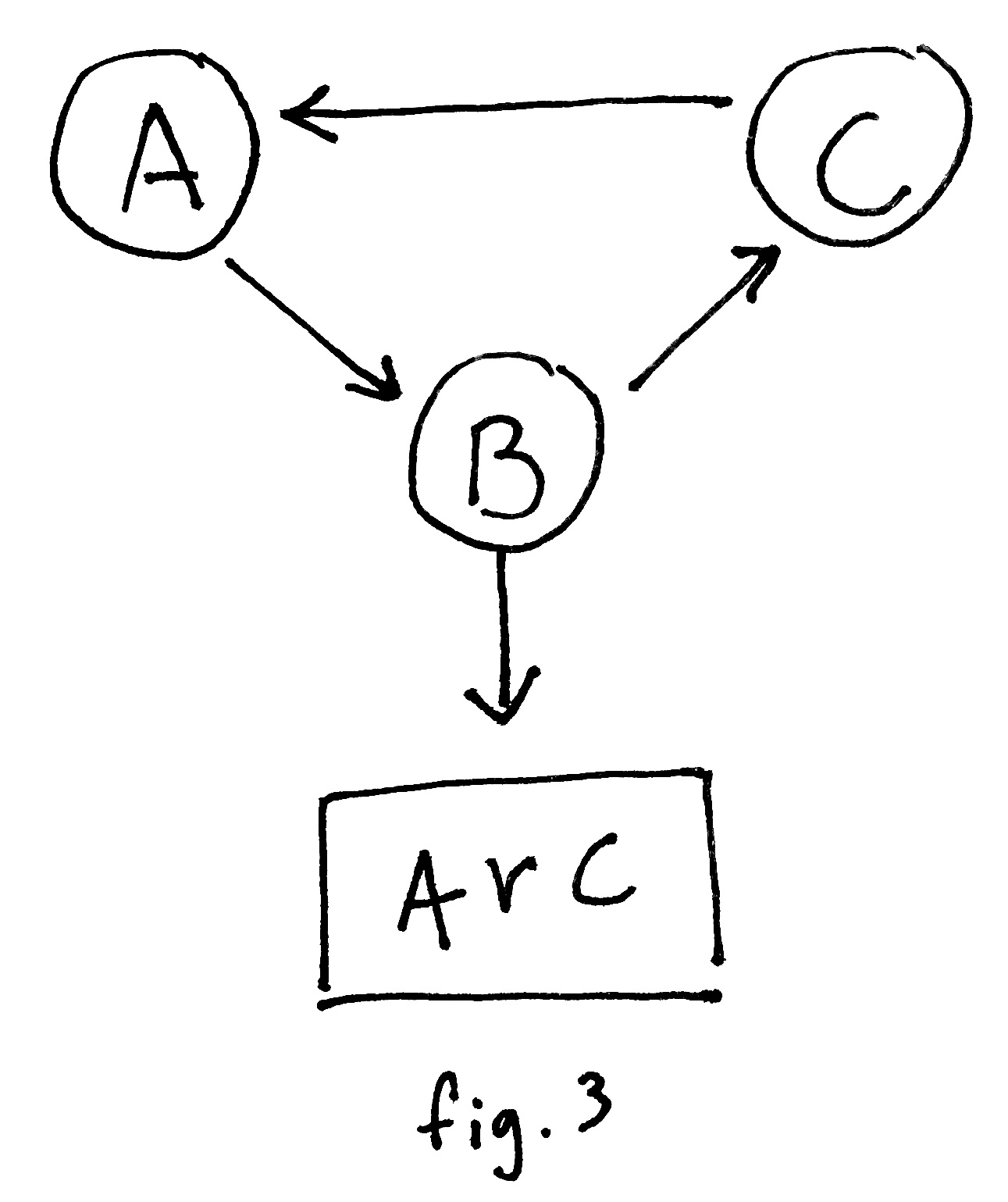
A data structure with three nodes: A, B, C and Arc, with four edges: A->B, B->C, B->Arc, C->A

The following unit test replicates it:

#[cfg(test)]
mod test {
    use super::*;
    use crate::gc::*;
    use std::sync::Arc;

    #[tokio::test]
    async fn cycles() {
        #[derive(Default, Trace)]
        struct Cyclic {
            next: Option<Gc<Cyclic>>,
            out: Option<Arc<()>>,
        }

        let out_ptr = Arc::new(());

        let a = Gc::new(Cyclic::default());
        let b = Gc::new(Cyclic::default());
        let c = Gc::new(Cyclic::default());

        // a -> b -> c -
        // ^----------/
        a.write().await.next = Some(b.clone());
        b.write().await.next = Some(c.clone());
        b.write().await.out = Some(out_ptr.clone());
        c.write().await.next = Some(a.clone());

        assert_eq!(Arc::strong_count(&out_ptr), 2);

        drop(a);
        drop(b);
        drop(c);

        let mut mutation_buffer_rx = MUTATION_BUFFER
            .get_or_init(MutationBuffer::default)
            .mutation_buffer_rx
            .lock()
            .unwrap()
            .take()
            .unwrap();
        let mut mutation_buffer = Vec::new();

        unsafe {
            process_mutation_buffer(&mut mutation_buffer).await;
            process_cycles();
            process_cycles();
        }

        assert_eq!(Arc::strong_count(&out_ptr), 1);
    }
}

Footnotes

1

One example of where this might come up is that Gc<dyn FnMut(&'static T)> is a subtype of for<'a> Gc<dyn FnMut(&'a T)>.

2

See here for more information.

3

More accurately, the reference count is one plus the difference between any call to a function of the form fn(&Gc) -> Gc such as the returned Gc has a copy of the pointer in the argument.

4

Now, if we were able to construct a Gc manually, i.e. by manually instanciating its fields with a copied NonNull, our invariant would not hold. But Gc’s field is private, and thus we can be assured that a Gc can only be created by user code via the new - which instantiates a new Gc with a ref count of one - or clone functions - which increment the reference count. Since drop only runs when a variable is no longer live, we know that it corresponds to a decrement in the ref count. Drop is not guaranteed to be invoked for an object, a user could call forget with the object and its destructor will not be run. But practically speaking, the destructor for an object is pretty much always going to be run.

5

See here and here

8

But even if they weren’t, since they are, a correct to the spec implementation of Scheme must be able to recognize such cyclical data structures and garbage collect them when appropriate.

6

I found a link to the paper here

7

You may find that some of these functions are different than how they are described in the paper. I found a bug in the MarkGray function, which didn’t properly decrement every node like the sync algorithm does. Similarly, the Scan algorithm incorrectly groups the if statements.